Translate this page into:
Statistical approaches to make sense of data in biology and medicine
*Corresponding author: S. S. Prakash, Department of Biochemistry, Christian Medical College, Vellore, Tamil Nadu, India. sspkmc2k@yahoo.com;
-
Received: ,
Accepted: ,
How to cite this article: Prakash SS. Statistical approaches to make sense of data in biology and medicine. Indian J Med Sci 2022;74:103-5.
Abstract
There are four major paradigms in statistics: Frequentist, Bayesian, likelihood, and modeling. A quadrangle approach that makes use of all these four paradigms is proposed to get a complete understanding of any biological phenomenon. Each of these paradigms can be used to study different aspects of a biological phenomenon. The elements are defined here as an observer, observed, and context, and the model generated should have information derived from these three elements. They can be analyzed, respectively, by Bayesian, frequentist, likelihood, and modeling methods. There is a continuous debate on frequentist and Bayesian approaches in statistics. Biologists often use frequentist methods whereas clinicians are interested in Bayesian methods. In this article, the debate on both these approaches has been discussed in light of understanding uncertainty. The Dempster-Shafer theory addresses the relationship between belief and plausibility but has been criticized for producing counterintuitive results in conflict situations. It is argued here that this can be resolved by inferring that frequentist and Bayesian approaches are inverse to each other.
Keywords
Biological data
Basic scientist
Clinician
Statistics
Modeling
Making sense of biological data is challenging due to its complexity and variability.[1] This can be systematically analyzed by locating where a researcher’s interest is. This will help in choosing the appropriate statistical methods.[2] There are basically three elements that need to be considered; observer, observed, and context. “Observer” is defined here as the sample or the system for which the data are generated. This could be an organism such as a human, a tissue, a cell, an organelle or even a protein or a gene of interest. ‘Observed” refers to the data that are generated from the observer. Many types of data can be generated from each one of the above entities described depending on the researcher’s interest. Context refers to the milieu in which the data are generated. The context may or not mimic the context in real life where the conclusions derived from the research will be extrapolated.
In statistical analysis, the “observer” can be analyzed by Bayesian approaches, the “observed” by frequentist approaches, and context by likelihood approaches. Those who are interested in modeling biological processes may have to include information on all these three aspects and then the fitness of the model needs to be ascertained [Figure 1].[3] A model with incomplete information on one or two of these elements may be incomplete. The information obtained from many models can then be combined and analyzed together to propose a theory. As more information and more models are added, the theory can be fine-tuned.
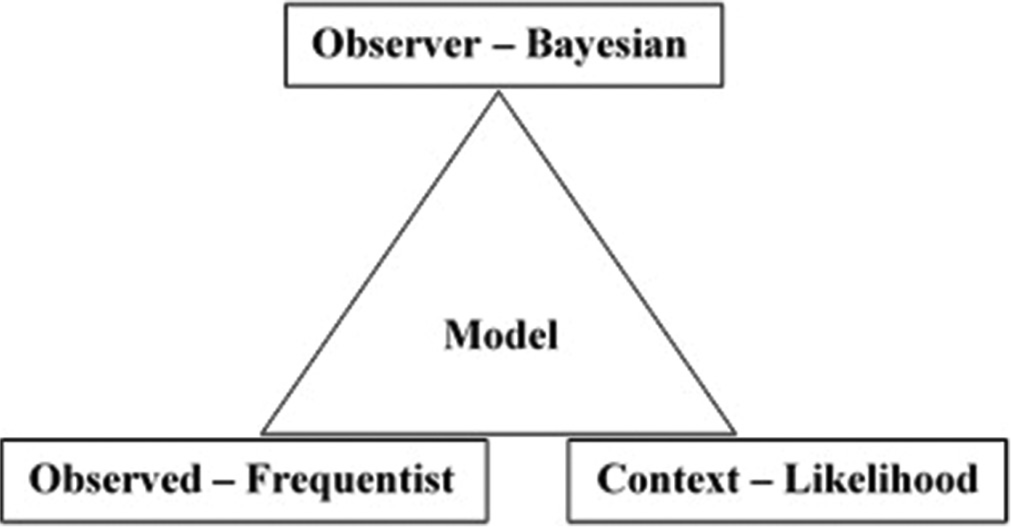
- Observer refers to the system for which data are collected. Observed is the data collected from the observer. Context refers to the milieu in which the data are collected. Each of these can be studied by the different paradigms in statistics as indicated. The model represents the theory which should include information on all three aspects of an observer, observed, and context.
Statistical analysis is both subjective and objective. Most of the statistical tests are aimed to find out the probability of finding a relationship.[4] Objectivists and subjectivists would prefer to adopt the frequentist or Bayesian approach, respectively.[5] The conflict situations are the ones, where there are chances of having counterintuitive results.[6] The situation with maximal plausibility but minimal belief would go well with the subjectivist while the situation with minimal plausibility but with maximal belief would go well with the objectivist, and not vice-versa leading to a difference of opinion.[7] Dempster (2014) has discussed the role of Dempster-Shafer theory in statistical inference examining the relationship between belief and plausibility which are mathematical functions of evidence.[8] This approach has implications for the analysis of data in biology and medicine.[9,10]
The inverse relationship between Bayesian and frequentist statistics can be understood by their sequence of approaching a problem. A Bayesian approach follows the sequence of why-how-what whereas the sequence of the frequentist approach would be what-how-why. As can be seen from the sequences, they are inverse to each other which provides the same meaning in a different direction and not reverse of each other as is frequently thought. A Bayesian is interested in understanding the process while a frequentist is interested in understanding the entity. It would be quite clear from this that both the entity and the process need to be understood for complete understanding of the truth.
There are different aspects of statistical association that researchers may rely on to implicate causation in biology and medicine.[11] A good guideline to follow will be that of the nine aspects set out by Sir Austin Bradford Hill, one of the greatest medical epidemiologists and statisticians.[12] This has found wide acceptance and application in several situations.[13] It would appear that frequentist and Bayesian statisticians might differ in which of the nine items proposed by Hill they could rely on. I presume that frequentists would pay more attention to the strength, consistency, specificity, and temporality of association as important for causation. Whereas Bayesians would place more weightage on biological gradient, plausibility, coherence, analogy, and experiment for causation. All these items are relevant and some may have more weightage than others depending on the context. It is, hence, ideal that both frequentist and Bayesian approaches are looked at, as they provide information which are inverse to each other.
The conflict and contrast mentioned in the above paragraphs can be better understood with a hypothetical example. Three researchers are interested in understanding the phenomenon of early morning rising by humans. The null hypotheses of each of the researchers are given below.
Researcher 1: Drinking coffee has no effect on early morning rising.
Researcher 2: There is no difference between early morning rising between males and females.
Researcher 3: Early morning rising has no relation to the season of the year.
Researcher 1 is interested to know whether drinking coffee is associated with early morning rising. In this case, the researcher would analyze the observers’ characteristics using a frequentist approach. Researcher 2 is interested in studying one of the characteristics of the observed, that is, gender, and would assess whether there is a difference between males and females in the early morning rising. An important but frequently forgotten third aspect is the context in which the data are generated and whether the relationships obtained would hold good if the context is different. Hence, the results of Researcher 3 concerning the context (in this case, season of the year) are an important piece of the puzzle to understand the phenomena of early morning rising. A model on early morning rising would be useful only when the results from all three researchers are used to construct it. Each of the studies would lack some data and hence the results of many related studies would have to be collected. A theory would take shape when information from many models is put together which is likely to provide explanations for all the data available.
In medicine, the characteristics and approaches of Researcher 1 are typically that of a basic scientist while Researcher 2 is that of a clinician. A basic scientist believes that a protein or gene of interest could be related to a phenomenon and to test this belief, the researcher resorts to the frequentist approach. A challenge for a basic scientist would be when the researcher has to resort to the Bayesian approach when analyzing a large microarray or gene expression dataset where the research question would take the form of “what is the probability of the gene or protein of interest to be related to the phenomenon being studied?”[14] This change in approach requires the basic scientist to pay attention to the elements of the observer and the context which would be challenging. Similarly, clinicians are interested in studying the likelihood (probability) or plausibility of a patient having a particular disease, or the effectiveness of a treatment given.[15] The information that a clinician would depend on will be the results of an average group of similar patients. The challenge would be when the clinician asks the question “what is the chance of a particular patient to have a disease or to be cured of the disease by the treatment given?” This is challenging because the clinician would require a frequentist approach.
I sincerely hope that considering Bayesian and frequentist as inverse approaches to one another would clear some air of the debate between these two approaches. The inference obtained from both these approaches is conveying the same truth in different ways. It is important that both these aspects are looked at in all situations and especially so in conflict situations. Applying Hill’s 9 points of view would further strengthen the statistical association to causation.
Declaration of patient consent
Patients’ consent not required as there are no patients in this study.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
References
- Common statistical pitfalls in basic science research. J Am Heart Assoc. 2016;5:e004142.
- [CrossRef] [PubMed] [Google Scholar]
- The interplay of bayesian and frequentist analysis. Stat Sci. 2004;19:58-80.
- [CrossRef] [Google Scholar]
- Frequentist properties of Bayesian posterior probabilities of phylogenetic trees under simple and complex substitution models. Syst Biol. 2004;53:904-13.
- [CrossRef] [PubMed] [Google Scholar]
- Possibility theory and statistical reasoning. Comput Stat Data Anal. 2006;51:47-69.
- [CrossRef] [Google Scholar]
- On the correspondence between frequentist and Bayesian tests. Commun Stat Theory Methods. 2018;47:3477-87.
- [CrossRef] [Google Scholar]
- Conflict management in Dempster-Shafer theory using the degree of falsity. Int J Approx Reason. 2011;52:449-60.
- [CrossRef] [Google Scholar]
- Dempster-Shafer theory and statistical inference with weak beliefs. Stat Sci. 2010;25:72-87.
- [CrossRef] [Google Scholar]
- Statistical inference from a Dempster-Shafer perspective. Past Present Future Stat Sci 2014:275-88.
- [Google Scholar]
- Application of Dempster-Shafer theory in dose response outcome analysis. Phys Med Biol. 2012;57:5575-85.
- [CrossRef] [PubMed] [Google Scholar]
- A framework for intelligent medical diagnosis using the theory of evidence. Knowledge Based Syst. 2002;15:77-84.
- [CrossRef] [Google Scholar]
- Statistical association and causation: Contributions of different types of evidence. JAMA. 2011;305:1134-5.
- [CrossRef] [PubMed] [Google Scholar]
- The environment and disease: Association or causation? Proc R Soc Med. 1965;58:295-300.
- [CrossRef] [Google Scholar]
- Applying the Bradford Hill criteria in the 21st century: How data integration has changed causal inference in molecular epidemiology. Emerg Themes Epidemiol. 2015;12:14.
- [CrossRef] [PubMed] [Google Scholar]
- Bayesian statistical methods for genetic association studies. Nat Rev Genet. 2009;10:681-90.
- [CrossRef] [PubMed] [Google Scholar]
- Bayesian statistics in medicine: A 25 year review. Stat Med. 2006;25:3589-631.
- [CrossRef] [PubMed] [Google Scholar]






